有限温量子体系的张量网络方法

　　张量网络方法是研究量子多体问题的利器。为了和有限温度下的实验测量建立直接的联系，同时也为了更好地刻画热涨落和量子涨落共存时所发生的丰富物理现象，有必要发展针对有限温量子体系的张量网络算法。这方面早期的代表性工作是物理所向涛研究员与上海交大王孝群教授等在九十年代中期所发展的转移矩阵重正化群方法。在那之后的二十多年里，新方法层出不穷。

最近，中国科学院物理研究所/北京凝聚态物理国家研究中心凝聚态理论与材料计算重点实验室T03组的王磊研究员，与北京大学物理学院国际量子材料科学中心的博士生唐维、徳累斯顿工业大学的涂鸿浩助理教授合作，提出了一类应用于有限温量子体系的张量网络方法。该方法借鉴了转移矩阵重整化群的思路，通过求解转移矩阵的最大本征态来研究体系的热力学性质。不同之处在于，新方法直接工作在连续的虚时间极限，从而利用了最近十年所发展的连续张量网络结构。

对比于此前提出的多种有限温张量网络方法，新方法主要特点是1）可以直接处理无限大的长程相互作用体系；2）可以直接在实频率计算低能局域谱函数。利用这些特点，作者研究了一维平方反比相互作用的量子伊辛模型以及准一维的量子伊辛模型在量子临界点附近的局域磁化率和零频谱函数的行为。将来，这些进展可用于预测阻错磁性和关联费米子体系的核磁共振实验中测得的自旋-晶格弛豫时间，以帮助理解体系有限温的低能激发性质。

该工作近期发表于物理评论快报（Phys. Rev. Lett. 125, 170604 (2020)）。文章链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.125.170604。基于PyTorch的开源代码实现：https://github.com/TensorBFS/cMPO。该工作得到了科技部 （2016YFA0300603，2016YFA0302400） 和国家自然科学基金委（11774398）的资助。

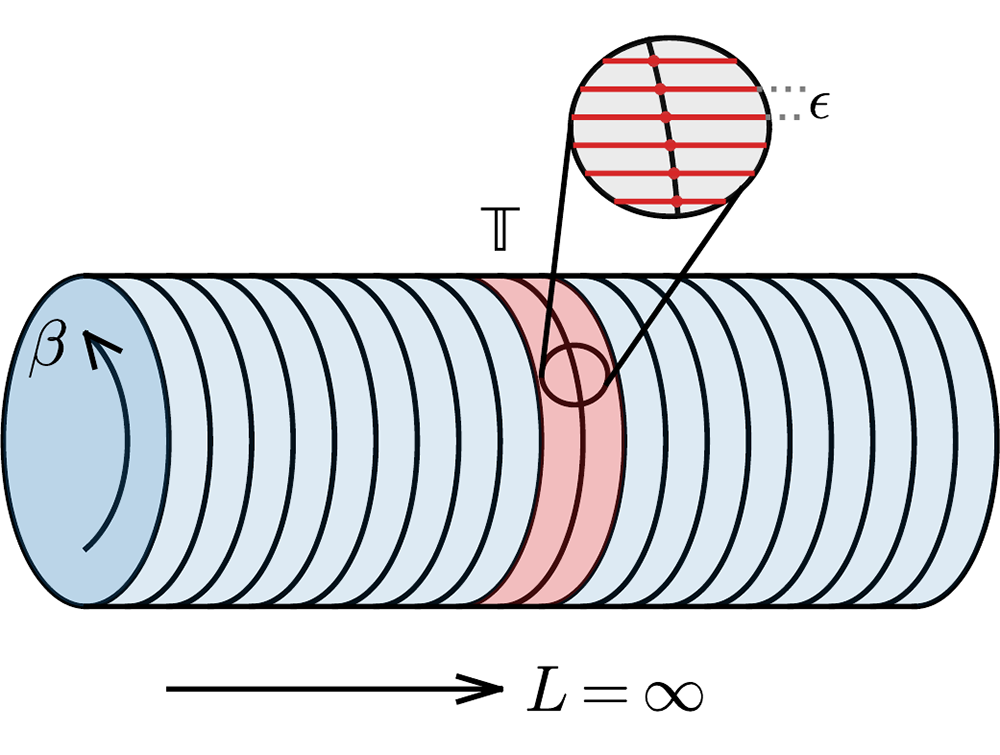
配分函数的连续虚时间张量网络表示