转角石墨烯有效模型理论研究取得进展
去年,《自然》杂志接连发表了两篇关于转角石墨烯的文章[1, 2],指出将两层单层石墨烯材料,扭转到特殊的角度,并辅以电场调控载流子浓度,体系在低温下可以产生超导现象,这一发现激起了世界范围内研究转角石墨烯系统的热潮。目前该领域还处于方兴未艾阶段,很多的实验观测没有公认的理论解释。比如在系统处在电中性时,原本导电性很强的石墨烯会变为绝缘体。有效连续模型可以计算转角石墨烯系统在不同角度下的能带图,人们发现在接近"魔角"时,电中性点附近的能带十分平坦,这些不稳定的平带是绝缘相和超导相出现的原因,但是由于系统的关联电子效应,在模型意义上没有近似的严格结果,需要考虑量子多体效应的数值计算来回答。
行列式量子蒙特卡洛方法是处理相互作用费米子体系的严格数值方法,并且易于实现大规模并行计算,在研究强关联电子体系中新奇的相与相变中发挥着重要作用。人们根据转角石墨烯连续有效模型得出的能带图,进一步抽象出一个格点紧束缚模型 [3],这就为使用量子蒙特卡洛等数值方法研究转角石墨烯有效晶格模型提供了可能。
近日,中国科学院物理研究所/北京凝聚态物理国家研究中心博士生廖元达、中科院物理所研究员孟子杨和香港科技大学/加州大学圣地亚哥分校博士后许霄琰组成的研究团队,利用投影量子蒙特卡洛方法,在如上所述的转角石墨烯有效晶格模型中考虑电子之间的强关联效应,详细研究了该有效模型在电中性点的基态相图(如图1所示)。他们发现,考虑六角格子的团簇电荷相互作用U,当相互作用较小时,系统处在狄拉克半金属态(Dirac semi-metal, DSM)。随着相互作用强度U的增加,狄拉克费米子的费米速度被重整化,直到U/t=25.1(2)处,系统的低能描述中出现了一个质量项,狄拉克锥处打开能隙,系统经历一个连续相变从DSM态转变为六格共振价键固体相(plaquette valence bond soild, pVBS)。经过详细的数值分析(如图2,图3),发现该连续相变属于三维 N = 4 Gross-Neveu手性XY普适类,具有涌现连续对称性,是金属态到绝缘体态的相变。他们进一步发现,当继续增强相互作用强度直到U/t=46,系统再次发生相变,从pVBS进入柱状共振价键固体相(columnar valence bond solid, cVBS)。该团队仔细研究了系统在相变点附近的动能、VBS的序参量等物理量(如图4),确定了该相变为一级相变,而在 pVBS与cVBS的交界处,如在一级相变的两相共存区中,边界上有拓扑保护的边界态存在。
这项工作填补了转角石墨烯模型研究中没有严格考虑量子多体效应工作的空白,为从量子临界涨落的角度理解转角石墨烯中新奇的实验结果提供思路,指出了运用大规模数值计算辅以有效晶格模型分析研究转角石墨烯系统的方向。相关研究成果近期发表在Phys. Rev. Lett. 123, 157601 (2019)。这项工作得到了科技部重点研发计划2016YFA0300502,中科院先导专项XDB28000000,国家自然科学基金委项目11574359,以及香港特别行政区研究资助局Grant 17303019,C6026-16W的支持。研究所进行的大规模并行计算,在中科院物理所量子模拟科学中心,国家超级计算天津中心的天河一号平台,国家超级计算广州中心天河二号平台上进行。研究团队特别感谢国家超算天津中心应用研发部孟祥飞部长、菅晓东工程师,国家超算广州中心应用推广部王栋部长、崔颖妍工程师等人的有力支持和配合。
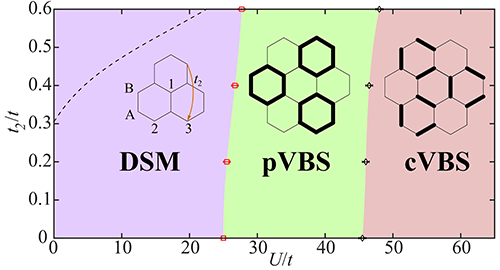 |
| 图1:转角石墨烯有效格点模型在电中性点随着团簇电荷相互作用U/t 的相图。 |
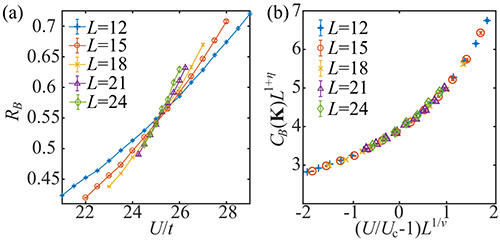 |
| 图2:(a). DSM-pVBS相变的键强关联比值之间的cross data,由此可以确定相变点在U/t=25.1(2)。(b). VBS态结构序参量的data collapse,由此可以定出来临界指数η=0.80(2),ν=1.01(3),符合三维 N = 4 Gross-Neveu手性XY普适类,具有涌现连续对称性。 |
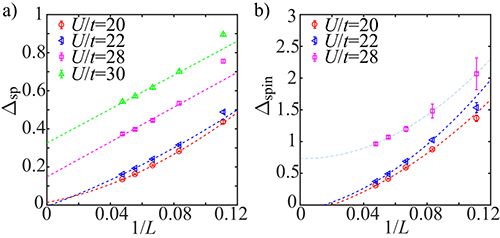 |
| 图3:DSM-pVBS相变是金属到绝缘体相变。 |
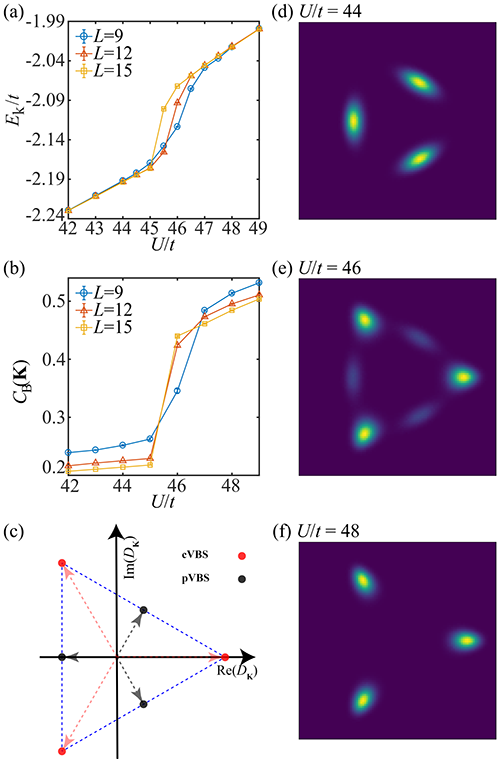 |
| 图4:两个不同VBS态之间的转变。序参量的 histogram 显示了两种共振价键绝缘体内部结构的不同。 |
参考文献:
[1] Y. Cao, V. Fatemi, A. Demir, S. Fang, S. L. Tomarken, J. Y. Luo, J. D. Sanchez-Yamagishi, K. Watanabe, T. Taniguchi, E. Kaxiras, R. C. Ashoori, and P. Jarillo-Herrero, Nature (London) 556, 80 (2018).
[2] Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras, and P. Jarillo-Herrero, Nature (London) 556, 43 (2018).
[3] M. Koshino, N. F. Q. Yuan, T. Koretsune, M. Ochi, K. Kuroki, and L. Fu, Phys. Rev. X 8, 031087 (2018).
