纽结半金属
日常生活中,我们几乎天天都要和纽结打交道: 从简单地系鞋带,到费力地解开莫名缠绕的耳机线,再到不得不狠心地剪断不小心碰一起的两条鱼线。 在数学里, 纽结被数学家们抽象出来发展成了一个重要的数学概念,对纽结的研究已经成为数学拓扑学的一个重要分支。为了完成对不同纽结的分类,大量的数学工具被发掘出来,比如琼斯多项式(Jones polynomial)。
和许多重要数学工具一样,纽结理论也在物理中找到了位置。纽结理论是研究拓扑量子场论和 拓扑弦理论的重要数学工具,也是量子拓扑计算和信息研究领域的一个重要理论基础。但是,到目前为止,纽结理论在物理中的应用还是局限在基础理论的框架内,似乎很难直接关联到实际物理系统和材料的研究中。
最近,中国科学院物理研究所/北京凝聚态物理国家研究中心凝聚态理论与材料计算重点实验室T06研究组胡江平研究员指导的博士生杨哲森,和物理所方辰研究员,以及国科大卡弗里理论科学中心邱靖凯研究员合作提出了可以用纽结理论的琼斯多项式去分类一类重要的量子材料:纽结半金属—包括近年发现的受对称性保护的厄米节线(nodal line)半金属和不受任何对称性保护的非厄米奇异线(exceptional line)半金属。
在这些纽结半金属中,能带的简并会在三维布里渊区中形成丰富结构,比如环,链,或者是非平凡的纽结。如何系统的分类和刻画这些非平凡的物理结构呢?
对这个问题的回答, 研究人员借鉴了过去研究陈绝缘体(Chern insulator)的方式:陈数的改变可以通过分析在相变点附近的狄拉克方程的质量项得到。在相变点附近,狄拉克质量项控制着布里渊区贝里曲率(Berry curvature)的变化,陈数的改变可以通过计算布里渊区内所有狄拉克点附近的质量项的变化之和求得。
研究人员注意到,在纽结半金属中,也存在着相同的物理图像。在纽结相变点附近,节线或者奇异线的局域演化可以和琼斯多项式的整体变化一一对应联系起来。相变点对应的节线存在一些离散的节线相交点,比如数字8可以看作是一个临界点,它有一个节线相交点。通过分析这些相交点附近节线的局域演化,就可以得到对应的琼斯多项式的整体变化。这些变化同时也会和系统的低能物理变化联系起来。因此这项研究为进一步研究纽结半金属这类量子材料的物性和开发其未来可能的应用提拱了理论基础。
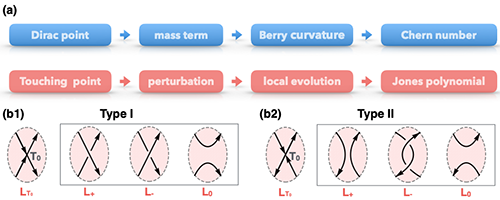 |
| 图1. 陈绝缘体和纽结半金属的对应(a)以及整体的拓扑性质和特殊点的局域性质的对应(b)。 |
 |
| 图2. 有四个相交点的临界相和几个对应的微扰生成的纽结相。 |
相关研究成果发表于物理评论快报(Phys. Rev. Lett. 124, 186402(2020)), 并且被选为编辑推荐的论文(Editor's Suggestion)。论文链接https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.124.186402。工作得到国家自然科学基金和科技部科研项目的资助。
