它山之石,可以攻玉——太赫兹二维相干光谱学打开探索量子自旋液体的新窗口
量子自旋液体是一种出现在量子磁体中的新奇物态。与通常磁性体系相比,量子自旋液体呈现出许多独特的物理现象,特别是所谓的分数化(fractionalization)现象。通常磁性体系中的准粒子是磁振子,携带一个单元的自旋角动量(自旋量子数为1)。量子自旋液体中的准粒子是自旋子(spinon),携带半个单元的自旋角动量(自旋量子数为1/2)。可以认为,自旋子是将磁振子"一分为二"而得到的。
自旋子的这种一分为二的特性是自旋子的主要实验特征。实验中探测自旋子,需利用外部扰动(如非弹性中子散射中的中子、太赫兹光谱学中的光子等)将自旋子激发出来,检测这些准粒子的动量和能量吸收,从中提取关于它们的信息。以太赫兹光谱为例,光子的能量和动量被体系吸收,并激发出自旋子。由于前述自旋子"一分为二"的特性,自旋子只能成对产生和湮灭(图一a)。这意味着,被吸收的光子动量和能量必须分配给这一对自旋子,而动量和能量的分配方式多种多样。每一种分配方式均会在太赫兹光谱中表现为一个尖锐的吸收峰,而前述多个分配方式则导致多个吸收峰。这些吸收峰拥挤在一起,最后总的效果就是一个缺乏个体特征的连续吸收谱(图一b)。
自旋子的这种连续吸收谱(continuum)被当作是自旋子存在的实验证据。但是连续谱给进一步分析自旋子的物理性质带来了挑战。连续谱来自于多个吸收峰的组合,因此掩盖了这些吸收峰本征的线宽与线型,也就难以进一步分析自旋子激发的谱学特性。在材料样品或者实验条件不理想的情况下,这种缺乏显著特征的吸收谱使得实验工作者难以仅凭谱学数据判断体系中是否存在自旋子这种准粒子。
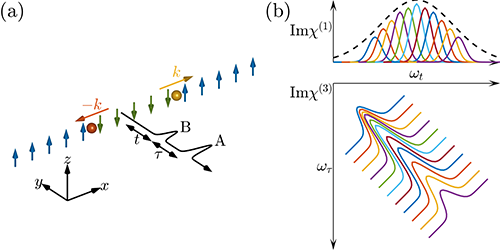
图一,太赫兹二维相干谱学示意图。(a)太赫兹二维相干谱学用一个太赫兹脉冲A激发体系中一对自旋子,用另一个太赫兹脉冲B探测它们。(b)自旋子在常规太赫兹光谱中表现为连续吸收谱,但在二维相干光谱中能展现出它们的本征线宽和线型。(来自文献[1])。
最近,中国科学院物理研究所/北京凝聚态物理国家研究中心凝聚态理论与材料计算实验室的万源副研究员与美国约翰霍普金斯大学物理系的实验学家Peter Armitage教授从理论上提出,太赫兹二维相干谱学(terahertz two-dimensional coherent spectroscopy)这种新兴实验技术可以给自旋子探测这个长期难题打开突破口 [1]。红外波段的二维相干谱学是一个相对成熟的实验技术,被广泛应用到分子物理、化学和生物物理等领域 [2]。近些年来,二维相干谱学被拓展到太赫兹波段 [3]。太赫兹二维相干谱学用一个太赫兹脉冲激发体系,用另一个太赫兹脉冲探测体系中的非线性光学响应,得到的光谱是激励频率和探测频率这两个频率的二维函数。
万源与Armitage的研究发现,自旋子的太赫兹二维光谱中存在一个类似于光子回波(photon echo)的"自旋子回波"(spinon echo)信号,该自旋子回波信号可以用来拆解前述的连续谱,并提取自旋子动力学的新信息。其背后的物理机制与光子回波区分均匀展宽(homogeneous broadening)与非均匀展宽(inhomogeneous broadening)的物理机制类似。具体来说,在太赫兹二维相干谱学中,前述的自旋子对的吸收峰被展布到一个二维频率平面上,这些吸收峰沿着平面对角线方向拥挤在一起。但是,沿着反对角线方向,这些吸收峰的本征线宽则被直接揭示出来(图一b)。
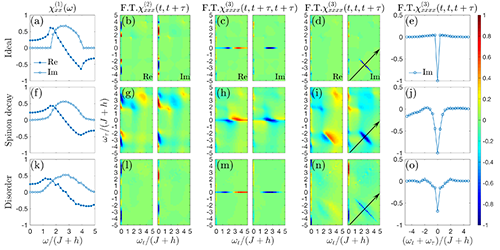
图二:量子伊辛自旋链中自旋子的一维光谱(左起第一列)和二维(第二到四列)相干光谱。自旋子回波信号出现的通道展示在第四列,其反对角线方向的信号 宽度展示在第五列。从上到下,第一行到第三行,分别对应于理想自旋链、存在准粒子衰减的自旋链和存在无序的情形。(来自文献[1])。
万源与Armitage以量子伊辛(Ising)自旋链这个模型系统为例,解析计算了这个体系的太赫兹二维相干光谱,具体阐明这项实验技术如何解析该体系中的自旋子连续谱,并进一步揭示自旋子的动力学。在完全理想的量子伊辛链中,自旋子为严格本征态,其准粒子寿命为无穷。对应的,在二维光谱中,自旋子回波信号在反对角线方向的宽度为零(图二,第一行)。当自旋子的准粒子寿命有限时,自旋子回波信号沿着反对角线方向展宽,其信号宽度反比于准粒子寿命(图二,第二行)。最后,当体系存在无序,但是准粒子寿命依然是无穷时,反对角线方向展宽依然为零,不受无序的干扰(图二,第三列)。这些理论预言,可以直接运用到以铌酸钴(CoNb2O6)为代表的量子伊辛链材料中去 [4]。相应的实验工作目前正在进行中。
参考文献:
[1] Yuan Wan and N.P. Armitage, Phys. Rev. Lett. 122, 257401 (2019).
[2] S. Mukamel, Principles of Nonlinear Optical Spectroscopy (Oxford University Press, New York, 1999); P. Hamm and M. Zanni, Concepts and Methods of 2D Infrared Spectroscopy (Cambridge University Press, Cambridge, England, 2011); 翁羽翔, 陈海龙等编著,《超快激光光谱原理与技术基础》(化学工业出版社,2013).
[3] M. Woerner, W. Kuehn, P. Bowlan, K. Reimann, and T. Elsaesser, New J. Phys. 15, 025039 (2013).
[4] R. Coldea, D.A. Tennant, E.M. Wheeler, E. Wawrzynska, D. Prabhakaran, M. Telling, K. Habicht, P. Smeibidl, and K. Kiefer, Science 327, 177 (2010).
